Le langage C

Nous avons étudié à la section précédente la syntaxe des déclarations des pointeurs. Dans le cas le plus simple, cette syntaxe est

    type *variable

Si par la suite on affecte à une telle variable l'adresse d'un certain objet, on fait référence à ce dernier par l'expression :

        *variable

Par exemple, l'expression

    char *p;

définit la variable p comme « pointeur vers un char ». Lorsqu'elle aura été correctement initialisée, elle contiendra l'adresse d'un caractère, auquel on pourra faire référence par l'expression

*p

Initialisation des pointeurs. Un pointeur contient en principe une adresse valide. Il existe trois manières sûres de donner une telle valeur à un pointeur :

1. Prendre l'adresse d'une variable existant par ailleurs. Exemple, déclaration :

    

   Sélectionnez

   type x, *p;

   Initialisation :

    

   Sélectionnez

   p = &x;

   p contient maintenant une adresse valide, l'adresse de la variable x. Par la suite, les expressions x et *p désigneront le même objet (le contenu de x).

2. Provoquer l'allocation d'un nouvel espace, c'est-à-dire allouer dynamiquement une variable anonyme.
   Exemple, déclaration :

    

   Sélectionnez

   type *p;
   Initialisation :
   p = malloc(sizeof(type));

   Après cette instruction, une variable tout à fait analogue à la variable x de l'exemple précédent existe. Comme dans l'exemple précédent, *p en désigne le contenu. La différence est qu'ici elle n'a pas de nom propre : si la valeur de p venait à être altérée (sans avoir été auparavant sauvegardée dans un autre pointeur), la variable pointée deviendrait inaccessible et serait définitivement perdue.

3. Obtenir une valeur par des calculs légitimes sur des pointeurs. Par exemple, comme on le verra bientôt, avec les déclarations

type t[10], *p, *q;

suivies de l'initialisation

p = &t[0]; (ou tout simplement p = t; )

l'expression

q = p + 3;

affecte à q l'adresse du quatrième élément du tableau t, c'est-à-dire &t[3].

Il existe aussi une manière risquée, en tout cas non portable, de donner une valeur à un pointeur : lui affecter une constante ou une expression numérique, dans le style de :

p = (struct machin *) 0x2A3E;

De telles expressions, indispensables dans certaines fonctions de bas niveau (contrôle d'organes matériels, etc.), rendent non portables les programmes ou elles figurent. Elles doivent donc être évitées chaque fois que cela est possible.

À propos de la taille des pointeurs et celle des entiers. Une expression comme l'affectation ci-dessus soulève un autre problème : existe-t-il une relation entre la taille d'un nombre entier (types int et unsigned int) et celle d'un pointeur ? Le langage ne prescrit rien à ce sujet ; il est donc parfois erroné et toujours dangereux de supposer qu'un entier puisse contenir un pointeur. Cette question peut sembler très secondaire, l'utilisation de variables entières pour conserver ou transmettre des pointeurs paraissant bien marginale. Or c'est ce qu'on fait, peut-être sans s'en rendre compte, lorsqu'on appelle une fonction qui renvoie un pointeur sans avoir préalablement déclaré la fonction. Par exemple, supposons que sans avoir déclaré la fonction malloc (ni inclus le fichier <stdlib.h>) on écrive l'affectation

p = (struct machin *) malloc(sizeof(struct machin));

Le compilateur rencontrant malloc pour la première fois, il postule que cette fonction renvoie un int et insère à cet endroit le code qui convertit un entier en un pointeur. Cette conversion peut fournir un résultat tout à fait erroné. Notamment, sur un système où les entiers occupent deux octets et les pointeurs quatre, les deux octets hauts du résultat de malloc seront purement et simplement remplacés par zéro. La question est d'autant plus vicieuse que le programme ci-dessus se comportera correctement sur tous les systèmes dans lesquels les entiers et les pointeurs ont la même taille.

Certaines fonctions de la bibliothèque, comme malloc, rendent comme résultat une « adresse quelconque », à charge pour l'utilisateur de la convertir en l'adresse spécifique qui lui convient. La question est : comment déclarer de tels pointeurs peu typés ou pas typés du tout ?

Le C original n'ayant rien prévu à ce sujet, la tradition s'était créée de prendre le type char * pour « pointeur vers n'importe quoi ». En effet, sur beaucoup de systèmes les adresses des objets de taille non unitaire supportent des contraintes d'alignement (les short aux adresses paires, les long aux adresses multiples de quatre, etc.), alors que les adresses des caractères sont les seules à ne subir aucune restriction.

Le C ANSI introduit un type spécifique pour représenter de telles adresses génériques : le type void *. Ce type est compatible avec tout autre type pointeur : n'importe quel pointeur peut être affecté à une variable de type void * et réciproquement 42. Par exemple, le fichier standard <stdlib.h> contient la déclaration suivante

de la fonction malloc :
void *malloc(size_t size);

Appel :

p = malloc(sizeof(struct machin));

Le pointeur NULL. Une des principales applications des pointeurs est la mise en œuvre de structures récursives de taille variable : listes chainées de longueur inconnue, arbres de profondeur quelconque, etc. Pour réaliser ces structures, il est nécessaire de posséder une valeur de pointeur, distincte de toute adresse valide, représentant la fin de liste, la structure vide, etc.

C garantit qu'aucun objet valide ne se trouve à l'adresse 0 et l'entier 0 est compatible avec tout type pointeur. Cette valeur peut donc être utilisée comme la valeur conventionnelle du « pointeur qui ne pointe vers rien » ; c'est l'équivalent en C de la constante nil de Pascal. En pratique on utilise plutôt la constante NULL qui est définie dans le fichier <stddef.h> :

#define NULL ((void *) 0)

⁴²Avec une protection supplémentaire : le type void étant incompatible avec tous les autres types, l'objet pointé par une variable déclarée de type void * ne pourra pas être utilisé tant que la variable n'aura pas été convertie en un type pointeur précis.

Arithmétique. Certaines des opérations arithmétiques définies sur les nombres gardent un sens lorsque l'un des opérandes ou les deux sont des adresses :

• l'addition et la soustraction d'un nombre entier à une adresse ;
• la soustraction de deux adresses (de types rigoureusement identiques).

L'idée de base de ces extensions est la suivante : si exp exprime l'adresse d'un certain objet O1 alors exp+1 exprime l'adresse de l'objet de même type que O1 qui se trouverait dans la mémoire immédiatement après O1 et exp¡1 l'adresse de celui qui se trouverait immédiatement avant.

De manière analogue, si exp1 et exp2 sont les adresses respectives de deux objets O1 et O2 de même type et contigus (O2 après O1), il semble naturel de donner à exp2-exp1 la valeur 1.

L'arithmétique des adresses découle de ces remarques. D'un point de vue technique, ajouter 1 à un pointeur c'est le considérer momentanément comme un entier et lui ajouter une fois la taille de l'objet pointé. On peut aussi dire cela de la manière suivante : exp1 et exp2 étant deux expressions de type « adresse d'un objet de type T » et n une expression entière, nous avons :

exp1 + n ≡ (T *) ((unsigned long) exp1 + n*sizeof(T))

et

exp2 - exp1 ≡ ((unsigned long) exp2 - (unsigned long) exp1) / sizeof(T)

L'indexation. Il découle des explications précédentes que l'arithmétique des adresses ne se justifie que si on peut considérer un pointeur p comme l'adresse d'un élément t[i₀] d'un tableau, éventuellement fictif. On peut alors interpréter p + i comme l'adresse de t[i₀ + i] et q - p comme l'écart entre les indices correspondant à ces deux éléments. Les pointeurs avec leur arithmétique et l'accès aux éléments des tableaux sont donc des concepts très voisins. En réalité il y a bien plus qu'un simple lien de voisinage entre ces deux concepts, car l'un est la définition de l'autre :

Soit exp une expression quelconque de type adresse et ind une expression entière. Par définition, l'expression :

*(exp + ind)

se note :

exp[ind]

On en déduit que si on a l'une ou l'autre des déclarations

type t[100];

ou

type *t;

alors dans un cas comme dans l'autre on peut écrire indifféremment

t[0] ou *t

ou

t[i] ou *(t + i)

Bien entendu, un programme est plus facile à lire si on montre une certaine constance dans le choix des notations.

Exemple. Le programme suivant parcourt un tableau en utilisant un pointeur :

char s[10] = "Hello";
main() {
char *p = s;
while (*p != '\0')
fputc(*p++, stdout);
}

int *p, t[100];

introduisent p comme une variable pointeur et t comme une constante pointeur. Ainsi, les expressions p = t et p++ sont légitimes, mais t = p et t++ sont illégales, car elles tentent de modifier une « non variable » (un nom de tableau n'est pas une lvalue).

char s[] = "Bonsoir";

et

char *t = "Bonsoir";

s est (l'adresse d') un tableau de caractères (figure 8)

tandis que t est l'adresse d'un (tableau de) caractère(s) (figure 9)

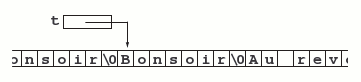
On pourra référencer ces caractères indifféremment par s[i], *(s + i), t[i] ou *(t + i). Cependant, dans le premier cas le compilateur a alloué un vrai tableau de 8 caractères, et y a copié la chaine donnée ; dans le second cas, la chaine a été rangée avec les autres constantes littérales et le compilateur n'a alloué qu'une variable de type pointeur dans laquelle il a rangé l'adresse de cette constante. Par suite, s n'est pas une variable, mais *s, s[i] et *(s + i) en sont, tandis que t est une variable, mais *t, t[i] et *(t + i) n'en sont pas 43.

À ce propos, voir aussi la section 5.1.3.

L'arithmétique des adresses permet d'améliorer l'efficacité de certains traitements de tableaux 44, en mettant à profit le fait que l'indirection est plus rapide que l'indexation. Autrement dit, l'accès à une donnée à travers une expression de la forme

*p

est réputée (légèrement) plus rapide que l'accès à la même donnée à travers l'expression

*(q + i) (ou, ce qui est la même chose, q[i])

Développons un exemple classique : la fonction strcpy(dest, srce) copie la chaine de caractères srce dans l'espace pointé par dest.

Première forme :

char *strcpy(char dest[], char srce[]) {
register int i = 0;
while ((dest[i] = srce[i]) != '\0')
i++;
return dest;
}

Deuxième forme :

char *strcpy(char *dest, char *srce) {
register char *d = dest, *s = srce;
while ((*d++ = *s++) != '\0')
;
return dest;
}

La deuxième forme est plus efficace, car on y a supprimé l'indexation. Pour s'en convaincre, il suffit de considérer que la boucle qui figure dans la première forme équivaut à :

while ((*(dest + i) = *(srce + i)) != '\0')
i++;

⁴³C'est uniquement d'un point de vue technique que ces expressions ne sont pas des variables, car du point de vue de la syntaxe elles sont des lvalue tout à fait légitimes et le compilateur ne nous interdira pas de les faire apparaitre à gauche d'une affectation.

⁴⁴Bien sûr, il s'agit de petites économies dont le bénéfice ne se fait sentir que lorsqu'elles s'appliquent à des parties des programmes qui sont vraiment critiques, c'est-à-dire exécutées de manière très fréquente.

L'équivalence entre les tableaux et les pointeurs permet de réaliser des tableaux dynamiques, c'est-à-dire des tableaux dont la taille n'est pas connue au moment de la compilation, mais uniquement lors de l'exécution, lorsque le tableau commence à exister.

Pour cela il suffit de

• remplacer la déclaration du tableau par celle d'un pointeur ;
• allouer l'espace à l'exécution, avant toute utilisation du tableau, par un appel de malloc ;
• dans le cas d'un tableau local, libérer l'espace à la fin de l'utilisation.

Pour tout le reste, l'utilisation de ces tableaux dynamiques est identique à celle des tableaux normaux (ce qui, pour le programmeur, est une très bonne nouvelle !). Exemple : la fonction ci-dessous calcule dans un tableau la N^eme ligne du triangle de Pascal 45 et s'en sert dans des calculs auxquels nous ne nous intéressons pas ici. On notera qu'une seule ligne diffère entre la version à tableau statique et celle avec tableau dynamique.

Programmation avec un tableau ordinaire (statique) :

void Blaise(int N) {
    int n, p, i;
    int tab[N_MAX + 1]; /* N_MAX est une constante connue à la compilation */
 
    for (n = 0; n <= N; n++) {
        tab[0] = tab[n] = 1;
        for (p = n - 1; p > 0; p--)
            tab[p] += + tab[p - 1];
                /* exploitation de tab ; par exemple, affichage : */
        for (i = 0; i <= n; i++)
            printf("]", tab[i]);
        printf("\n");
    }
}

Programmation avec un tableau dynamique :

void Blaise(int N) {
        int n, p, i;
        int *tab; /* ici, pas besoin de constante connue à la compilation */
 
        tab = malloc((N + 1) * sizeof(int));
        if (tab == NULL)
            return;
        for (n = 0; n <= N; n++) {
            tab[0] = tab[n] = 1;
            for (p = n - 1; p > 0; p--)
                tab[p] += + tab[p - 1];
                /* exploitation de tab ; par exemple, affichage : */
        for (i = 0; i <= n; i++)
            printf("]", tab[i]);
        printf("\n");
    }
    free(tab); /* à ne pas oublier ( tab est une variable locale) */
}

⁴⁵Rappelons que les coefficients de la n^e ligne du triangle de Pascal sont définis récursivement à partir de ceux de la n-1^eme ligne par : C^p_n = C^p-1_n-1 + C^p_n-1

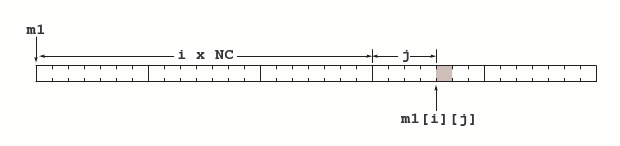
Réflexions sur la double indexation. Supposons que nous ayons à écrire un programme qui opère sur des matrices à NL lignes et NC colonnes. La déclaration d'une telle matrice est facile à construire (cf. section V.D.1) :

tableau de NL tableau de NC float         m1
tableau de NC float                 (m1)[NL] ou m1[NL]
float                         (m1[NL])[NC] ou m1[NL][NC]

Un élément particulier de cette matrice sera noté m1[i][j]. D'après ce que nous savons déjà, on peut l'interpréter de la manière suivante 46 :

m1[i][j]
= *(m1[i] + j)
= *(float *)((unsigned int) m1[i] + j * sizeof(float))

Le problème est : avec la déclaration que nous avons donnée, que signifie m1[i] ? Il est intéressant de constater que cette expression n'est pas une lvalue, puisqu'elle est de type « tableau de… », mais que, à part cela, elle est traitée comme un élément d'un tableau ordinaire. Autrement dit, si on supposait avoir la déclaration

typedef float LIGNE[NC]; /* LIGNE = tableau de NC float */

alors m1[i] serait une expression de type LIGNE valant :

m1[i]
= *(m1 + i)
= *(LIGNE *)((unsigned) m1 + i * sizeof(LIGNE))
= *(LIGNE *)((unsigned) m1 + i * NC * sizeof(float))

En oubliant pour un instant les types des pointeurs, il nous reste

m1[i][j] = *(m1 + (i * NC + j) * sizeof(float))

Nous retrouvons l'expression classique i * NC + j caractérisant l'accès à un élément m_i,j d'une matrice NL*NC. Cette expression traduit la disposition « par lignes » des tableaux rectangulaires, comme le montre la figure 10.

Étudions une autre manière d'accéder aux éléments de cette même matrice. Soit les déclarations

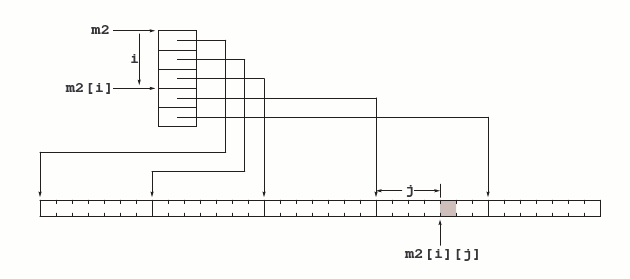
float m1[NL][NC], *m2[NL];

La deuxième se lit, compte tenu des priorités : float *(m2[NL]). La variable m2 est donc déclarée comme un tableau de NL pointeurs vers des nombres flottants. Pour réaliser la matrice dont nous avons besoin, il nous suffit d'initialiser correctement ces pointeurs : chacun sera l'adresse d'une ligne de la matrice précédente. Nous aurons la configuration de la figure 11.

Il est remarquable qu'un élément de la nouvelle « matrice » ainsi déclarée se note encore

m2[i][j]

mais maintenant, cette expression se traduira (en continuant à négliger les conversions des types pointeurs) par :

m2[i][j]
    = *(m2[i] + j * sizeof(float))
    = *(*(m2 + i * sizeof(float *)) + j * sizeof(float))

Les multiplications par sizeof(float) et sizeof(float *) sont réalisées de manière très rapide par les calculateurs (ce sont des multiplications par des puissances de 2), nous pouvons les ignorer. Il reste que nous avons remplacé « m1 + i * NC + j » par « *(m2 + i) + j ». Nous avons donc bien éliminé une « vraie » multiplication : notre deuxième manière est plus efficace. En contrepartie nous occupons un peu plus d'espace (les NL pointeurs supplémentaires).

De plus, il nous faut initialiser le tableau de pointeurs m2. La matrice m1 existant par ailleurs, cela se fait ici par une expression d'une étonnante simplicité :

for (i = 0; i < NL; i++)
m2[i] = m1[i];

⁴⁶Pour alléger les formules, nous supposons ici que la taille d'un int, et donc celle d'un unsigned, est égale à celle d'un pointeur.

Les considérations précédentes montrent pourquoi dans la réalisation d'une matrice dynamique on devra renoncer au mécanisme de double indexation ordinaire. En effet, NC doit être connu à la compilation pour que l'expression i * NC + j ait un sens.

Or nous sommes maintenant parfaitement équipés pour réaliser une telle matrice. Supposons que la fonction void unCalcul(int nl, int nc) implémente un algorithme qui requiert une matrice locale à nl lignes et nc colonnes.

Version statique :

#define NL 20
#define NC 30
...
void unCalcul(int nl, int nc) {
    double mat[NL][NC]; /* en espérant que nl · NL et nc · NC */
    int i, j;
        /* utilisation de la matrice mat. Par exemple : */
for (i = 0; i < nl; i++)
    for (j = 0; j < nc; j++)
        mat[i][j] = 0;
etc.
}

Version dynamique (par souci de clarté nous y avons omis la détection des échecs de malloc) :

void unCalcul(int nl, int nc) {
 double **mat;
 int i, j;
    /* initialisation des pointeurs */
 mat = malloc(nl * sizeof(double *));
 for (i = 0; i < nl; i++)
 mat[i] = malloc(nc * sizeof(double));
    /* utilisation de la matrice mat. Par exemple : */
 for (i = 0; i < nl; i++)
 for (j = 0; j < nc; j++)
 mat[i][j] = 0;
 etc.
    /* libération (indispensable dans le cas d'une variable locale) */
 for (i = 0; i < nl; i++)
 free(mat[i]);
 free(mat);
}

Dans cette manière de procéder, les lignes de la matrice sont allouées à l'occasion de nl appels distincts de malloc. La matrice est réalisée par des morceaux de mémoire éparpillée, comme le montre la figure 12.

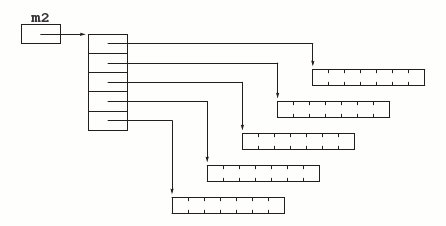
Variante : lignes contigües. Une légère variante consiste à allouer d'un seul coup toute la mémoire nécessaire aux lignes de la matrice. La structure de la matrice ressemble alors à celle de la figure 11 :

int unCalcul(int nl, int nc) {
    double **mat, *espace;
    int i, j;
        /* initialisation des pointeurs */
    mat = malloc(nl * sizeof(double *));
if (mat == NULL)
    return 0; /* échec */
        espace = malloc(nl * nc * sizeof(double));
if (espace == NULL) {
    free(mat);
        return 0; /* échec */
    }
for (i = 0; i < nl; i++)
mat[i] = espace + i * nc;
        /* utilisation de la matrice mat. Par exemple : */
for (i = 0; i < nl; i++)
for (j = 0; j < nc; j++)
mat[i][j] = 0;
etc.
        /* libération (indispensable dans le cas d'une variable locale) */
    free(espace);
    free(mat);
    return 1; /* succès */
}

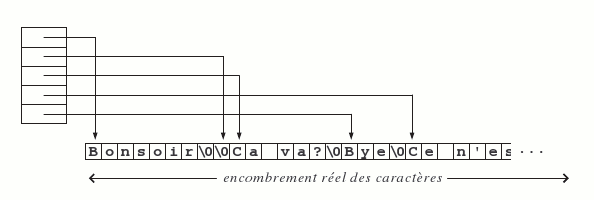
Le remplacement d'un tableau à deux indices par un tableau de pointeurs se révèle encore plus utile dans le traitement des tableaux de chaines de caractères. Ici, cette technique entraine une économie de place substantielle, puisqu'elle permet de remplacer un tableau rectangulaire dont la largeur est déterminée par la plus grande longueur possible d'une chaine (avec un espace inoccupé très important) comme celui de la figure 13, par un espace linéaire dans lequel chaque chaine n'occupe que la place qui lui est nécessaire, comme le montre la figure 14.

Nous allons illustrer cette méthodologie par un exemple très simple, mais tout à fait typique. Notre programme lit des lignes de caractères au terminal et les range dans une table, jusqu'à la rencontre de la fin de fichier ou la lecture d'une ligne vide. Ensuite, il ordonne les lignes lues ; finalement il affiche les lignes ordonnées. Les lignes lues sont rangées les unes à la suite des autres dans un tableau unique, nommé espace, dont le pointeur libre indique la première place disponible. La table des mots, notée mots, est une table de renvois dans espace. La figure 14 illustre ces structures de données. Notez que le tri se fait en ordonnant la table des pointeurs ; les caractères eux-mêmes ne sont nullement déplacés.

Les fonctions gets (lecture de chaine), puts (écriture de chaine), strcmp (comparaison de chaines) et strlen (longueur d'une chaine) appartiennent à la bibliothèque standard et sont expliquées dans les sections suivantes.

#include <stdio.h>
#include <string.h>
 
#define MAXMOTS 100
#define MAXCARS 3000
 
char espace[MAXCARS];
char *libre = espace;
char *mots[MAXMOTS];
int nbr_mots = 0;
 
void tri(char *t[], int n) {
    for (;;) {
        int i, ok = 1;
        for (i = 1; i < n; i++)
            if (strcmp(t[i - 1], t[i]) > 0) {
                char *w = t[i - 1];
                t[i - 1] = t[i];
                t[i] = w;
                ok = 0;
        }
    if (ok)
    return;
    n--;
  }
}
 
void main(void) {
    int i;
    while(gets(libre) != NULL && *libre != '\0') {
        mots[nbr_mots++] = libre;
        libre += strlen(libre) + 1;
    }
    tri(mots, nbr_mots);
    for (i = 0; i < nbr_mots; i++)
        printf("%s\n", mots[i]);
}

char *messages[] = {
    "Fichier inexistant",
    "Volume ou repertoire inexistant",
    "Nom de fichier incorrect",
    "Erreur physique d'entree-sortie",
    "Autre erreur" };

La seule différence entre notre tableau mots et le tableau messages que créerait le compilateur par suite de la déclaration ci-dessus est la suivante : les éléments de mots sont des pointeurs vers un espace modifiable faisant partie de la mémoire attribuée pour les variables de notre programme, tandis que messages est fait de pointeurs vers des cellules de la « zone de constantes », espace non modifiable alloué et garni une fois pour toutes par le compilateur.

Nous avons vu que si un argument formel d'une fonction ou une variable externe est un tableau à un seul indice, alors l'indication du nombre de ses éléments est sans utilité puisqu'il n'y a pas d'allocation d'espace. Mais que se passe-t-il pour les tableaux à plusieurs indices ? Si un tableau a été déclaré
T table[N1][N2] ... [Nk-1][Nk] ;
(N1, N2, etc. sont des constantes) alors un accès comme

table[i1][i2] ... [ik-1][ik]

se traduit par *( (T*)table + i1 * N2 * N3 * ... * Nk + ... + ik-1 * Nk + ik ) Qu'il y ait ou non allocation d'espace, il faut que ce calcul puisse être effectué. D'où la règle générale : lorsqu'un argument formel d'une fonction est un tableau à plusieurs indices, la connaissance de la première dimension déclarée est sans utilité, mais les autres dimensions déclarées doivent être connues du compilateur. Pour un tableau à deux indices, cela donne : il est inutile d'indiquer combien il y a de lignes, mais il faut absolument que, en compilant la fonction, le compilateur connaisse la taille déclarée pour chaque ligne. Par exemple, la fonction suivante effectue la multiplication par un scalaire k de la matrice m déclarée NL * NC (deux constantes connues dans ce fichier) :

void k_fois(double k, double m[][NC]) {
    int i, j;
    for (i = 0; i < NL; i++)
        for (j = 0; j < NC; j++)
            m[i][j] *= k;
}

Remarque. Bien entendu, une autre solution aurait consisté à faire soi-même les calculs d'indice :

void k_fois(double k, void *m) {
int i, j;
for (i = 0; i < NL; i++)
for (j = 0; j < NC; j++)
*((double *) m + i * NC + j) *= k;
}

Tout ce qu'on y gagne est un programme bien plus difficile à lire !

En principe, les tableaux de C sont indexés à partir de zéro : sans qu'il soit nécessaire de le spécifier, un tableau T déclaré de taille N est fait des éléments T₀, T₁ … T_N-1. Nous avons vu que, dans la grande majorité des applications, cette convention est commode et fiable.

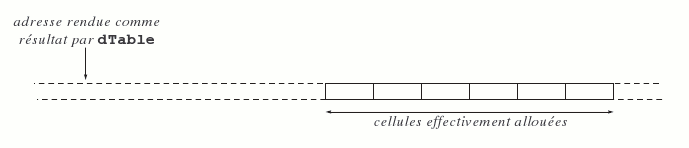
Il existe cependant des situations dans lesquelles on souhaiterait pouvoir noter les éléments d'un tableau T₁, T₂ … T_N ou, plus généralement, T_a, T_a+1 … T_b, a et b étant deux entiers quelconques vérifiant a · b. Nous allons voir que l'allocation dynamique fournit un moyen simple et pratique 47 pour utiliser de tels tableaux. Cas des tableaux à un indice. La fonction dTable48 crée un tableau d'éléments de type double dont les indices sont les entiers iMin, iMin+1… iMax :

double *dTable(int iMin, int iMax) {
double *res = malloc((iMax - iMin + 1) * sizeof(double));
if (res == NULL) {
erreurTable = 1;
return NULL;
}
erreurTable = 0;
return res - iMin;
}

(Si on avait besoin de tableaux de float, de int, etc. on écrirait des fonctions analogues fTable, iTable, etc.). La variable globale erreurTable est rendue nécessaire par le fait qu'un résultat NULL ne suffit pas ici à caractériser l'échec de l'allocation ; en effet, res - iMin peut être nul alors que l'allocation a réussi et res ≠ NULL. La figure 15 illustre le résultat rendu par la fonction précédente lors d'un appel comme dTable(5, 10).

0n accède aux éléments d'un tel tableau à l'aide d'un indice compris entre les valeurs indiquées, mais, à part cela, de manière tout à fait habituelle ; en particulier, sans aucune perte d'efficacité. Exemple d'utilisation :

...
double *t = dTable(5, 10);
...
for (i = 5; i <= 10; i++)
t[i] = 1000 + i;
...
for (i = 5; i <= 10; i++)
printf("%.1f\n", t[i]);
...

free(t);

générera certainement une erreur à l'exécution. Il aurait fallu définir une structure plus complexe qu'un simple tableau, incluant soit la valeur de iMin, soit celle de res (actuellement des variables locales de la fonction dTable) pour gérer correctement la libération ultérieure d'un tel tableau.

Cas des tableaux à plusieurs indices. Les remarques précédentes, avec celles faites à la section 6.2.4, suggèrent une manière de mettre en œuvre des matrices dont les lignes et les colonnes ne sont pas indexées à partir de zéro.

La fonction dMatrice crée une matrice dont les lignes sont indexées par les entiers lMin, lMin+1 … lMax et les colonnes sont indexées par les entiers cMin, cMin+1 … cMax :

double **dMatrice(int lMin, int lMax, int cMin, int cMax) {
    int nbLin, nbCol, i;
    double *espace, **lignes, *p;
 
    nbLin = lMax - lMin + 1;
    nbCol = cMax - cMin + 1;
    espace = malloc(nbLin * nbCol * sizeof(double));
    if (espace == NULL) {
        erreurTable = 1;
        return NULL;
    }
    lignes = malloc(nbLin * sizeof(double *));
    if (lignes == NULL) {
        erreurTable = 1;
        free(espace);
        return NULL;
    }
    p = espace - cMin;
    for (i = 0; i < nbLin; i++) {
        lignes[i] = p;
        p += nbCol;
    }
    erreurTable = 0;
    return lignes - lMin;
}

Comme précédemment, l'emploi de ces matrices ne s'accompagne d'aucune perte d'efficacité. Voici un exemple d'utilisation :

...
double **m = dMatrice(5, 10, -3, 3);
...
for (i = 5; i <= 10; i++)
    for (j = -3; j <= 3; j++)
        m[i][j] = 1000 * i + j;
...
for (i = 5; i <= 10; i++) {
    for (j = -3; j <= 3; j++)
        printf("%10.1f ", m[i][j]);
    printf("\n");
}
...

⁴⁷Nous expliquons ici une technique massivement employée dans la bibliothèque de calcul scientifique Numerical Recipes (°c Numerical Recipes Software) basée sur le livre Numerical Recipes in C (W. Press, S. Teukolsky, W. Vetterling et B. Flannery, Cambridge University Press, 1992).

⁴⁸D'obscures contraintes techniques, ayant perdu tout intérêt de nos jours, font que cette technique peut ne pas fonctionner dans les implantations de C sur d'anciennes plateformes, comme les PC à base de processeurs Intel antérieurs au 80286 (un lointain ancêtre du Pentium), dans lesquelles l'arithmétique des adresses subit des limitations drastiques.

Un dernier cas qui se présente parfois est celui où on doit écrire une fonction opérant sur des matrices ordinaires (c'est-à-dire non dynamiques) alors que leurs dimensions ne sont pas connues lors de la compilation. Par exemple, voici la fonction qui effectue le produit de deux matrices A et B en déposant le résultat dans une troisième matrice C. Les arguments nla et nca représentent le nombre effectif de lignes et de colonnes de A, tandis que ncb est le nombre effectif de colonnes de B. Les arguments dNca, dNcb et dNcc représentent les nombres de colonnes avec lesquels on a déclaré les matrices A, B et C respectivement.

void produitMatrices(double *A, double *B, double *C,
        int nla, int nca, int ncb, int dNca, int dNcb, int dNcc) {
    int i, j, k;
    double s;
 
    for (i = 0; i < nla; i++)
        for (j = 0; j < ncb; j++) {
            s = 0;
            for (k = 0; k < nca; k++) /*1*/
                s += A[i * dNca + k] * B[k * dNcb + j]; /*1*/
            C[i * dNcc + j] = s;
    }
}

Exemple d'appel (NLA, NCA, etc., sont des constantes introduites par des #define, tandis que nla, nca, etc. sont des variables) :

double A[NLA][NCA], B[NLB][NCB], C[NLC][NCC];
...
obtention des valeurs des variables nla, nca, etc., et des matrices A et B
...
produitMatrices(&A[0][0], &B[0][0], &C[0][0], nla, nca, ncb, NCA, NCB, NCC);
...

On notera que la fonction produitMatrices peut être optimisée en supprimant des multiplications qui sont faites dans la boucle la plus profonde (la seule qui doit nous intéresser, du point de vue de l'efficacité). Pour cela, il suffit de remplacer les deux lignes marquées /*1*/ par ceci (ia et ib sont des variables locales nouvelles) :

        ...
ia = i * dNca;                     /*2*/
ib = j;                         /*2*/
for (k = 0; k < nca; k++) {     /*2*/
    s += A[ia] * B[ib];         /*2*/
    ia += 1;                     /*2*/
    ib += dNcb;                 /*2*/
} /*2*/
...

En étudiant les déclarateurs complexes (section 5.4) nous avons appris que la syntaxe de C permettait de manipuler le type « fonction rendant un [objet de type] T » (T représente un autre type), cette périphrase constituant elle-même un déclarateur que le programmeur peut composer librement avec les autres déclarateurs, « adresse d'un [objet de type] T » et « tableau de [objets de type] T ». Tout cela suggère qu'en C on aura le droit de travailler avec des variables qui représentent des fonctions, des tableaux de fonctions, des fonctions renvoyant comme résultat d'autres fonctions, etc. Qu'en est-il exactement ?

Le concept le plus simple qu'on peut souhaiter dans ce domaine est celui de variable dont la valeur est une fonction. Il va falloir y renoncer, pour une raison facile à comprendre : la taille d'une fonction ne peut pas se déduire de son type49. C'est un inconvénient rédhibitoire, car toute définition de variable doit entrainer la réservation d'un espace mémoire pour en contenir la valeur, ce qui demande de connaitre combien d'octets sont nécessaires.

En revanche, le langage C permet d'utiliser un concept à peine plus complexe que le précédent : celui de variable dont la valeur est l'adresse d'une fonction. Il n'y a plus de problème de taille (la taille d'une adresse - ou pointeur - est constante), et la syntaxe pour déclarer une telle variable a déjà été expliquée dans la section sur les déclarateurs complexes (cf. section V.D). Exemple :

double (*uneFonction)(int n, double x);

Cet énoncé déclare uneFonction comme une variable (un pointeur) destinée à contenir des adresses de fonctions ayant deux arguments, un int et un double, et rendant une valeur double. Cette déclaration n'initialise pas uneFonction (sauf, si c'est une variable globale, avec la valeur 0, peu utile ici) et, à part le type des arguments et du résultat, ne laisse rien deviner sur les caractéristiques des fonctions dont uneFonction contiendra les adresses.

Si, par la suite, uneFonction reçoit l'adresse d'une fonction A pour valeur, alors l'expression suivante est correcte et représente un appel de φ (en supposant k de type int et u et v de type double) :

u = (*uneFonction)(k, v);

Comment le programmeur obtient-il des adresses de fonctions ? Il faut savoir que, de la même manière que le nom d'un tableau représente son adresse de base, le nom d'une fonction représente l'adresse de celle-ci. Ainsi, si on a la définition de fonction

double maFonction(int nbr, double val) {
/* etc. */
}

alors l'expression maFonction :

• possède le type « adresse d'une fonction ayant pour arguments un int et un double et rendant un double » ;
• a pour valeur l'adresse ou commence la fonction maFonction ;
• n'est pas une lvalue.

Par conséquent, l'affectation suivante est tout à fait légitime :

uneFonction = maFonction;

À partir de cette affectation (et tant qu'on n’aura pas changé la valeur de uneFonction) les appels de (*uneFonction) seront en fait des appels de maFonction.

Examinons deux applications de cela parmi les plus importantes.

⁴⁹Notez que, malgré les apparences, il n'est pas délirant de rapprocher les fonctions et les données. Une fois compilée (traduite en langage machine), une fonction est une suite d'octets qui occupe une portion de mémoire exactement comme, par exemple, un tableau de nombres. La principale différence est dans la possibilité ou l'impossibilité de prédire le nombre d'octets occupés.

Pour un tableau, par exemple, ce nombre découle sans ambigüité de la déclaration. Pour une fonction il ne dépend pas de la déclaration (qui ne précise que le type du résultat et le nombre et les types des arguments), mais du nombre d'instructions qui composent la fonction, c'est-à-dire de ce qu'elle fait et comment elle le fait.

Le problème des fonctions formelles, c'est-à-dire des fonctions arguments d'autres fonctions, est résolu en C par l'utilisation d'arguments de type « pointeur vers une fonction ».

Exemple 1 : résolution de f(x) = 0 par dichotomie. Si f est une fonction continue, définie sur un intervalle [ a … b ] telle que f(a) et f(b) ne sont pas de même signe, la fonction dicho recherche x_ε ∈ [ a … b ] telle qu'il existe x₀ ∈ [ a … b ] vérifiant |x_ε - x₀| < ε et f(x₀) = 0. En clair : dicho détermine x_ε, qui est une solution de l'équation f(x) = 0 si on tolère une erreur d'au plus ε.

Les arguments de la fonction dicho sont : les bornes a et b de l'intervalle de recherche, la précision " voulue et surtout la fonction f dont on cherche un zéro. Voici cette fonction :

double dicho(double a, double b, double eps, double (*f)(double)) {
    double x;             /* hypothèse : f(a) * f(b) <= 0 */
    if ((*f)(a) > 0) {
        x = a; a = b; b = x;
    }
    while (fabs(b - a) > eps) {
        x = (a + b) / 2;
        if ((*f)(x) < 0)
            a = x;
        else
            b = x;
    }
    return x;
}

L'argument f est déclaré comme un pointeur vers une fonction ; par conséquent *f est une fonction et (*f)(x) un appel de cette fonction. Si une fonction est le nom d'une fonction précédemment définie, changeant de signe sur l'intervalle [0, 1], un appel correct de dicho serait

x = dicho(0.0, 1.0, 1E-8, une_fonction);

Autre exemple du même tonneau

y = dicho(0.0, 3.0, 1E-10, cos);

Remarque. En syntaxe originale, ou « sans prototype », la fonction dicho s'écrirait

double dicho(a, b, eps, f)
double a, b, eps, (*f)();
{
etc. (la suite est la même)
}

Exemple 2 : utilisation de qsort. Reprenons notre programme de la section 6.2.5 (tri d'un tableau de chaines de caractères) en remplaçant la fonction de tri naïf par la fonction qsort de la bibliothèque standard. Cette fonction est expliquée à la section 8.4.2, elle trie un tableau par rapport à un critère quelconque. Si elle nous intéresse ici c'est parce qu'elle prend ce critère, représenté par une fonction, pour argument :

#include <stdio.h>
#include <string.h>
 
#define MAXMOTS 100
#define MAXCARS 3000
 
char espace[MAXCARS], *libre = espace;
char *mots[MAXMOTS];
int nbr_mots = 0;
    /* La déclaration suivante se trouve aussi dans <stdlib.h> : */
void qsort(void *base, size_t nmemb, size_t size,
int (*comp)(const void *, const void *));
int comparer(const void *a, const void *b) {
    /* Les arguments de cette fonction doivent être déclarés "void *" (voyez la */
    /* déclaration de qsort). En réalité, dans les appels de cette fonction que */
    /* nous faisons ici, a et b sont des adresses de "chaines", c'est-à-dire des */
    /* adresses d'adresses de char */
return strcmp(*(char **)a, *(char **)b);
}
 
main() {
    int i;
    while(gets(libre) != NULL && *libre != '\0') {
        mots[nbr_mots++] = libre;
        libre += strlen(libre) + 1;
    }
    qsort(mots, nbr_mots, sizeof(char *), comparer);
    for (i = 0; i < nbr_mots; i++)
        printf("%s\n", mots[i]);
}

• comparer figurant comme argument dans l'appel de qsort, son prototype doit correspondre exactement 50 à celui indiqué dans le prototype de qsort ;
• a et b, les arguments formels de comparer, étant de type void *, on ne peut accéder aux objets qu'ils pointent sans leur donner auparavant (à l'aide de l'opérateur de conversion de type) un type pointeur « utilisable » ;
• d'après la documentation de qsort, nous savons que comparer sera appelée avec deux adresses de chaines pour arguments effectifs ; une chaine étant de type char *, le type « adresse de chaine » est char **, ce qui explique la fa»con dont a et b apparaissent dans l'appel de strcmp.

⁵⁰En syntaxe « sans prototype », aucun contrôle n'est fait sur le type des arguments de comparer, et toute cette question est bien plus simple. Mais attention : quelle que soit la syntaxe employée, on ne peut pas ignorer le fait que comparer sera appelée (par qsort) avec pour arguments effectifs les adresses des chaines à comparer.

Le programme suivant montre l'utilisation d'un tableau d'adresses de fonctions : chaque élément du tableau table est formé de deux champs :

• le nom d'une fonction standard, sous forme de chaine de caractères ;
• l'adresse de la fonction correspondante.

Notre programme lit des lignes constituées d'un nom de fonction, suivi d'un ou plusieurs blancs, suivis d'un nombre réel ; il évalue et affiche alors la valeur de la fonction mentionnée appliquée au nombre donné. La frappe d'une ligne réduite au texte fin arrête le programme.

#include <stdio.h>
 
double sin(double), cos(double), exp(double), log(double);
 
struct {
    char *nom;
    double (*fon)(double);
} table[] = {
    "sin", sin,
    "cos", cos,
    "exp", exp,
    "log", log };
 
#define NBF (sizeof table / sizeof table[0])
 
main() {
    char nom[80];
    double x;
    int i;
    for(;;) {
        scanf("%s", nom);
        if (strcmp(nom, "fin") == 0)
            break;
    scanf("%lf", &x);
    for(i = 0; i < NBF && strcmp(table[i].nom, nom) != 0; i++)
        ;
    if (i < NBF)
        printf("%f\n", (*table[i].fon)(x));
    else
        printf("%s ???\n", nom);
    }
}

Voici une exécution de ce programme :

sin 1
0.841471
cos 1
0.540302
atn 1
atn ???
fin

soit en incluant un fichier dans lequel sont écrites ces déclarations :

#include <math.h>

À ce point de notre exposé, vous êtes en droit de trouver que les rôles respectifs des objets de type « fonction… » et des objets de type « adresse d'une fonction… » sont confus. Examinons une fonction bien ordinaire, sinus. La déclaration de cette fonction, extraite du fichier <math.h>, est :

double sin(double);

D'autre part, la définition d'une variable de type « adresse d'une fonction double à un argument double » est : double (*f)(double);

Voici l'initialisation de f par l'adresse de la fonction sin et deux appels équivalents de cette fonction (x, y et z sont des variables double) :

f = sin;
y = (*f)(x);
z = sin(x);

Quelle que soit la valeur de x, y et z reçoivent la même valeur. Pourtant, les trois lignes ci-dessus ne sont pas cohérentes. La première montre que f et sin sont de même type (à savoir « adresse d'une fonction… ») ; or f doit être déréférencé pour appeler la fonction, tandis que sin n'a pas besoin de l'être.

On peut comprendre la raison de cette incohérence. Après avoir constaté l'impossibilité de déclarer des variables de type « fonction… » , car une fonction n'a pas de taille définie, et donc l'obligation de passer par des variables « adresse de fonction… », on a voulu faire cohabiter la rigueur (un pointeur doit être déréférencé pour accéder à l'objet qu'il pointe) et la tradition (le sinus de x s'est toujours écrit sin(x)). Cela a conduit à définir l'opérateur d'appel de fonction aussi bien pour une expression de type « fonction… » que pour une expression de type « adresse d'une fonction… ». Ainsi, les deux expressions (*f)(x) et sin(x) sont correctes ; l'expérience montre que cette tolérance n'a pas de conséquences néfastes. Il n'en découle pas moins que les deux expressions

u = f(x);
v = (*sin)(x);

sont acceptées elles aussi (elles ont la même valeur que les précédentes).

Les structures récursives font référence à elles-mêmes. Elles sont principalement utilisées pour implanter des structures de données dont la définition formelle est un énoncé récursif. Parmi les plus fréquemment rencontrées : les listes et les arbres, comme les arbres binaires.

Par exemple, on peut donner la définition récursive suivante : un arbre binaire est

• soit un symbole conventionnel signifiant « la structure vide » ;
• soit un triplet ( valeur , filsg , filsd ) constitué d'une information dont la nature dépend du problème étudié et de deux descendants qui sont des arbres binaires.

Bien entendu, du point de vue technique il n'est pas possible de déclarer un champ d'une structure comme ayant le même type que la structure elle-même (une telle structure serait ipso facto de taille infinie !). On contourne cette difficulté en utilisant les pointeurs. Un arbre binaire est représenté par une adresse, qui est :

• soit l'adresse nulle ;
• soit l'adresse d'une structure constituée de trois champs : une information et deux descendants qui sont des adresses d'arbres binaires.

Typiquement, la déclaration d'une telle structure sera donc calquée sur la suivante :

struct noeud {
type valeur;
struct noeud *fils_gauche, *fils_droit;
};

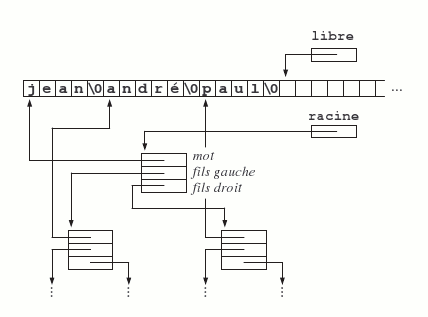
Le programme suivant effectue le même travail que celui du 6.2.5, mais à la place d'une table on utilise un arbre binaire de recherche (voir, par exemple, R. Sedgewick, Algorithmes en langage C, chapitre 14) pour ranger les mots. La structure de données mise en œuvre est représentée sur la figure 16.

#include <stdlib.h>
#include <stdio.h>
 
#define MAXCARS 3000 char
 
espace[MAXCARS], *libre = espace;
 
typedef struct noeud {
    char *mot;
    struct noeud *fils_gauche, *fils_droit;
} NOEUD, *POINTEUR;
 
POINTEUR alloc(char *m, POINTEUR g, POINTEUR d) {
    POINTEUR p = malloc(sizeof(NOEUD));
    p->mot = m;
    p->fils_gauche = g;
    p->fils_droit = d;
    return p;
}
 
POINTEUR insertion(POINTEUR r, char *mot) {
    if (r == NULL)
        r = alloc(mot, NULL, NULL);
    else
        if (strcmp(mot, r->mot) <= 0)
            r->fils_gauche = insertion(r->fils_gauche, mot);
    else
            r->fils_droit = insertion(r->fils_droit, mot);
 return r;
}

void parcours(POINTEUR r) {
if (r != NULL) {
parcours(r->fils_gauche);
printf("%s\n", r->mot);
parcours(r->fils_droit);
}
}
main() {
POINTEUR racine = NULL;
char *p;
p = gets(libre);
while(*p != '\0') {
libre += strlen(p) + 1;
racine = insertion(racine, p);
p = gets(libre);
}
parcours(racine);
}

Donnons-nous le problème suivant : représenter une « liste de familles » ; chaque famille est une « liste d'individus », avec la particularité que chaque individu fait référence à sa famille. Les structures famille et individu se pointent mutuellement, chacune intervenant dans la définition de l'autre. Comment les déclarer ?

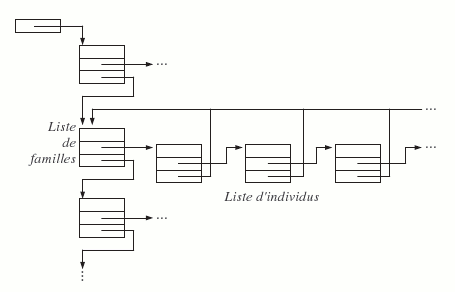
Pour résoudre ce problème, le compilateur C tolère qu'on déclare un pointeur vers une structure non encore définie. Plus précisément, si la structure ayant le nom indiqué n'a pas encore été déclarée, l'expression « struct nom » est légitime. Elle identifie un type incomplet et on peut l'utiliser à tout endroit ou sa taille n'est pas requise, notamment dans la déclaration d'un pointeur vers une telle structure. Cela nous permet de déclarer nos structures mutuellement récursives sous la forme :

typedef struct famille {
    char *nom;
    struct individu *membres;
    struct famille *famille_suivante;
} FAMILLE;
 
typedef struct individu {
    char *prenom;
    struct individu *membre_suivant;
    struct famille *famille;
} INDIVIDU;

Une autre solution aurait été :

typedef struct famille FAMILLE;
typedef struct individu INDIVIDU;
 
struct famille {
    char *nom;
    INDIVIDU *membres;
    FAMILLE *famille_suivante;
};
 
struct individu {
    char *prenom;
    INDIVIDU *membre_suivant;
    FAMILLE *famille;
};